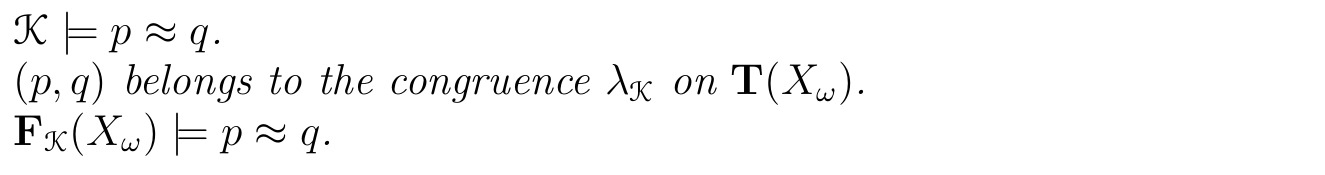
$\def\inj{\mathrm{in}}$ $\def\inji{\mathrm{in}_i}$

Preliminaries

Notation

The symbols $\mathbb{N}$, $\omega$, and nat are used interchangeably; they all denote the set of natural numbers.

If $m$ is a natural number, we write $m \colon \mathbb N$ and say "$m$ has type $\mathbb N$." (For the reader unfamiliar with type theory, it's safe in the beginning to think of this as meaning $m\in \mathbb N$.)

For $m \colon \mathbb N$, we denote and define $\underline{m} = \{0, 1, \dots, m-1\}$. Let $a = (a_0, a_1, \dots, a_{m-1})$ be an mtuple of elements from $A$.

(As explained in the post on composition of operations, the tuple $a$ may be identified with a function of type $\underline{m} \to A$, where $a(i) = a_i$, for each $i<m$.)

If $h \colon A \to A$, then $h\circ a : \underline{m} \to A$ is the function whose $i$-th coordinate is $(h\circ a)(i) = h(a(i)) = h(a_i)$, and we may formally identify the function $h \circ a : \underline{m} \to A$ with its "image tuple" $(h(a_0), h(a_1), \dots, h(a_{m-1}))$.

A signature $S = (F, \rho)$ consists of a set $F$ of operation symbols and a function $\rho \colon F \to \mathbb{N}$. We call $\rho f$ the arity of the symbol $f$.

If $A$ is a set and $f$ is a $\rho f$-ary operation on $A$, then we may write $f \colon A^{\rho f} \to A$. On the other hand, as the natural number $\rho f$ denotes the set $\{0, 1, \dots, \rho f -1\}$, a function $a \colon \rho f \to A$ can be identified with its graph, which is simply a $\rho f$-tuple of elements from $A$; that is, $a i : A$, for each $i: \rho f$. Then, by identifying the $\rho f$-th power $A^{\rho f}$ with the type $\rho f \to A$ of functions from $\{0, 1, \dots, \rho f -1\}$ to $A$, we thus identify the function type $A^{\rho f} \to A$ with the type $(\rho f \to A) \to A$.

Examples.
a. If $g \colon (\underline{m} \to A) \to A$ is an $\underline{m}$-ary operation on $A$ and if $a : \underline{m} \to A$, then $g a = g(a_0, a_1, \dots, a_{m-1})$ has type $A$.
b. If $f \colon (\rho f \to B) \to B$ is a $\rho f$-ary operation on $B$, if $a \colon \rho f \to A$ is a $\rho f$-tuple on $A$, and if $h \colon A \to B$, then of course $h \circ a \colon \rho f \to B$, so $f (h \circ a)$ has type $B$.

Generalized composition. We summarize in a single sentence the final result of our previous post on general composition. If $f\colon (\underline n \to A) \to A$ and if $g : \Pi_{i:\underline{n}} (\underline{k_i} \to A) \to A$ and $a : \Pi_{i : \underline{n}}(\underline{k_i} \to A)$, then $\mathbf{eval}\circ \mathbf{fork}(g)(a)$ has type $\underline{n} \to A$, which is the domain type of $f$; therefore, $f \circ (\mathbf{eval}\circ \mathbf{fork}(g) (a))$ has type $A$, as desired. See the post on general composition for details.

We summarize in a single sentence the final result of our previous post on general composition. If $f\colon (\underline n \to A) \to A$ and if $g : \Pi_{i:\underline{n}} (\underline{k_i} \to A) \to A$ and $a : \Pi_{i : \underline{n}}(\underline{k_i} \to A)$, then $\mathbf{eval}\circ \mathbf{fork}(g)(a)$ has type $\underline{n} \to A$, which is the domain type of $f$; therefore, $f \circ (\mathbf{eval}\circ \mathbf{fork}(g) (a))$ has type $A$, as desired. See the post on general composition post for details.

Elementary facts

Let $F$ be an endofunctor on Set and let $(A, f^A)$ and $(B, f^B)$ be $F$-algebras. (The F-algebras post explains what this means.)

1. Let $g$ and $h$ be $F$-homomorphisms from $(A, f^A)$ to $(B, f^B)$. That is $g \circ f^A = f^B \circ F g$ (similarly with $h$ in place of $g$). Let $E(g,h) = \{ a : A \mid g(a) = h(a) \}$. Then

   a. $E(g,h)$ is a subuniverse of $(A, f^A)$.

   b. If $X \subseteq A$ and $X$ generates $(A, f^A)$ and $g|_X= h|_X$, then $g = h$.

   c. If $A$ and $B$ are finite sets and $X$ generates $(A, f^A)$, then $|\mathrm{Hom}((A, f^A),(B, f^B))| \leq |B|^{|X|}$.

   Proof. Suppose there are $m$ operation symbols in the similarity type of the two algebras, and assume the $i$-th operation symbol has arity $k_i$. Then $F A : \coprod_{i=0}^{m-1}(\underline{k_i} \to A)$.

   a. Fix arbitrary $0\leq i< m$ and $a : \underline{k_i} \to E(g,h)$. We wish to show that $g (f^A (\inji a)) = h (f^A (\inji a))$, as this will show that $E(g,h)$ is closed under the $i$-th operation of $(A, f^A)$. (Since $i$ was arbitrary this will complete the proof.) But this is trivial since, by definition of an $F$-algebra homomorphism, we have $$(g \circ f^A)(\inji a) = (f^B \circ F g)(\inji a) = (f^B \circ F h)(\inji a) = (h \circ f^A)(\inji a).$$

   b. Suppose the subset $X \subseteq A$ generates $(A, f^A)$ and suppose $g|_X = h|_X$. Fix an arbitrary $a : A$. We show $g(a) = h(a)$. Since $X$ generates $(A, f^A)$, there exists a term $t$ and a tuple $x : \rho t \to X$ of generators such that $a = t^A x$. Therefore, since $F g = F h$ on $X$, we have $$g(a) = g(t^A x) = (t^B \circ F g)(x) = (t^B \circ F h)(x) = h(t^A x) = h(a).$$

   c. By b, a homomorphism is uniquely determined by its restriction to a generating set. If $X$ generates $(A, f^A)$, then, since there are exactly $|B|^{|X|}$ functions from $X$ to $B$, we have $|\mathrm{Hom}((A, f^A),(B, f^B))| \leq |B|^{|X|}$.

2. Suppose $g$ and $h$ are homomorphisms from $(A, f^A)$ to $(B, f^B)$ and from $(A, f^A)$ to $(C,f^C)$, respectively. Assume $g$ is surjective, and $\ker g \subseteq \ker h$. Then there exists a homomorphism $k$ from $(B, f^B)$ to $(C, f^C)$ such that $h = k \circ g$.

   Proof. Define $k\colon B \to C$ as follows: for each $b\in B$, choose (by Axiom of Choice!) $a_0\in g^{-1}\{b\}$ and let $k(b) = h(a_0)$. (Since $g$ is surjective, such an $a_0$ exists for each $b\in B$.) Fix $a \in A$. We show $h(a) = k g(a)$. Let $a_0$ be the element of $g^{-1}\{g(a)\}$ that we chose when defining $k$ at $b = g(a)$. That is, $k(b) = h(a_0)$. Then, $g(a_0) = b = g(a)$, so $(a_0, a) \in \ker g\subseteq \ker h$, so $h(a) = h(a_0) = k(b) = k g(a)$, as desired.

   To see that $k$ is a homomorphism, let there be $m$ operation symbols and let $0\leq i< m$ be arbitrary. Fix $b : \underline{k_i} \to B$ and $a : \underline{n} \to A$ be the respective representatives of the $g$-kernel classes $g^{-1}\{b(i)\}$ that we chose when defining $k$. Then, $$(f^C \circ F k) (b) = (f^C \circ F k) ((F g) a) = (f^C \circ F h) (a) = (h \circ f^A)(a) = (k g \circ f^A)(a).$$ $$(k \circ (g \circ f^A))(a) = (k \circ (f^B \circ F g))(a) = (k \circ f^B) ((F g)(a)) = (k \circ f^B)(b).$$

   Subalgebra generation

   Clones

3. Let $A$ be a set and $S = (F, \rho)$ a signature and suppose each $f\in F$ is a $(\rho f)$-ary operation on $A$. Define $$\begin{aligned} F_0 &= \operatorname{Proj}}}(A);\ F_{n+1} &= F_n \cup \{ f g \mid f \in F, g \colon \rho f \to (F_n \cap (\rho g \to A)) \}, \text{ for } n < \omega. \end{aligned}$$ Then $\operatorname{Clo}}}^A(F) = \bigcup_n F_n$.

   Terms and Free Algebras

4. Let $\rho$ be a similarity type.

   a. $\mathbf{T}_\rho(X)$ is generated by $X$.

   b. For every algebra $(A, f^A)$ of type $\rho$ and every function $h\colon X \to A$ there is a unique homomorphism $g\colon \mathbf{T}\rho(X) \to (A, f^A)$such that${{ \left.\kern-\nulldelimiterspace g \vphantom{\big|} \right|{X} }} = h$.

   Proof.* The definition of $\mathbf{T}_\rho(X)$ exactly parallels the construction in Theorem 1.14 (Bergman 2012). That accounts for (1). For (2), define $g(t)$ by induction on $|t|$. Suppose $|t| = 0$. Then $t \in X \cup {\mathcal{F}}}_0$. If $t \in X$ then define $g(t) = h(t)$. For $t \in {\mathcal{F}}}_0$, $g(t) = t^{(A, f^A)}$. Note that since $(A, f^A)$ is an algebra of type $\rho$ and $t$ is a nullary operation symbol, $t^{(A, f^A)}$ is defined.

   For the inductive step, let $|t| = n + 1$. Then $t = f(s_1, \dots, s_k)$ for some $f \in {\mathcal{F}}}_k$ and $s_1, \dots, s_k$ each of height at most $n$. We define $g(t) = f^{(A, f^A)}(g(s_1), \dots, g(s_k))$.

   By its very definition, $g$ is a homomorphism. Finally, the uniqueness of $g$ follows from Exercise 1.16.6 in Bergman (2012).

5. Let $(A, f^A)$ and $(B, f^B)$ be algebras of type $\rho$.

   a. For every $n$-ary term $t$ and homomorphism $g\colon (A, f^A) \to (B, f^B)$, $g(t^{(A, f^A)}(a_1,\dots, a_n)) = t^{(B, f^B)}(g(a_1),\dots, g(a_n))$.

   b. For every term $t \in T_\rho(X_\omega)$ and every $\theta \in \operatorname{Con}((A, f^A))}}$, $(A, f^A)\equiv_\theta (B, f^B)\implies t^{(A, f^A)}((A, f^A)) \equiv_\theta t^{(A, f^A)}((B, f^B))$.

   c. For every subset $Y$ of $A$, $$\operatorname{Sg}^{(A, f^A)}(Y)}} = \{ t^{(A, f^A)}(a_1,\dots, a_n) : t \in T(X_n), a_i \in Y, i \leq n < \omega\}.$$

   Proof. The first statement is an easy induction on $|t|$. The second statement follows from the first by taking $(B, f^B) = (A, f^A)/\theta$ and $g$ the canonical homomorphism. For the third statement, again by induction on the height of $t$, every subalgebra must be closed under the action of $t^{(A, f^A)}$. Thus the right-hand side is contained in the left. On the other hand, the right-hand side is clearly a subalgebra containing the elements of $Y$ (take $t = x_1$) from which the reverse inclusion follows.

Birkhoff's Theorem

Let $\rho$ be a similarity type. An identity of type $\rho$ is an ordered pair of terms, written $p \approx q$, from $T_\rho(X_\omega)$. Let $(A, f^A)$ be an algebra of type $\rho$. We say that $(A, f^A)$ satisfies $p\approx q$ if $p^{(A, f^A)} = q^{(A, f^A)}$. In this situation, we write $(A, f^A) \models p \approx q$. If $\mathcal{K}$ is a class of algebras of type $\rho$, we write $\mathcal{K} \models p \approx q$ if $\forall (A, f^A) \in \mathcal{K}$, $(A, f^A) \models p \approx q$. Finally, if $\Sigma$ is a set of equations, we write $\mathcal{K} \models \Sigma$ if every member of $\mathcal{K}$ satisfies every member of $\Sigma$.

Let $\mathcal{K}$ be a class of algebras and $\Sigma$ a set of equations, each of similarity type $\rho$. We define $\operatorname{Id}(\mathcal{K}) = \{p \approx q : \mathcal{K} \models p \approx q\}$ and $\operatorname{Mod}(\Sigma) = \{ (A, f^A) : (A, f^A) \models \Sigma \}$. Classes of the form $\operatorname{Mod}(\Sigma)$ are called equational classes, and $\Sigma$ is called an equational base or an axiomatization of the class. $\operatorname{Mod}(\Sigma)$ is called the class of models of $\Sigma$. Dually, a set of identities of the form $\operatorname{Id}(\mathcal{K})$ is called an equational theory.

1. For every class $\mathcal{K}$, each of the classes $\mathbf{S}(\mathcal{K})$, $\mathbf{H}(\mathcal{K})$, $\mathbf{P}(\mathcal{K})$, and $\mathbf{V}(\mathcal{K})$ satisfies exactly the same identities as does $\mathcal{K}$.

   (exercise)

2. $\mathcal{K} \models p \approx q$ if and only if for every $(A, f^A) \in \mathcal{K}$ and every $h\in \operatorname{Hom}(\mathbf{T}(X_\omega),(A, f^A))}}$, we have $h(p) = h(q)$.

   Proof. First assume that $\mathcal{K} \models p\approx q$. Pick $(A, f^A)$ and $h$ as in the theorem. Then $(A, f^A) \models p\approx q \implies p^{(A, f^A)} = q^{(A, f^A)} \implies p^{(A, f^A)}(h(x_1), \dots, h(x_n)) = q^{(A, f^A)}(h(x_1), \dots, h(x_n))$. Since $h$ is a homomorphism, we get $h(p^{(A, f^A)}(x_1, \dots, x_n)) = h(q^{(A, f^A)}(x_1, \dots, x_n))$, i.e., $h(p) = h(q)$.

   To prove the converse we must take any $(A, f^A) \in \mathcal{K}$ and $a_1, \dots, a_n \in A$ and show that $p^{(A, f^A)}(x_1, \dots, x_n) = q^{(A, f^A)}(x_1, \dots, x_n)$. Let $h_0 \colon X_\omega \to A$ be a function with $h_0(x_i) = a_i$ for $i\leq n$. By Theorem 4.21 (Bergman, 2012), $h_0$ extends to a homomorphism $h$ from $\mathbf{T}(X_\omega)$ to $(A, f^A)$. By assumption $h(p) = h(q)$. Since $h(p) = h(p^{(A, f^A)}(x_1, \dots, x_n)) = p^{(A, f^A)}(h(x_1), \dots, h(x_n)) = p^{(A, f^A)}(a_1,\dots, a_n)$ (and similarly for $q$) the result follows.

3. Let $\mathcal{K}$ be a class of algebras and $p \approx q$ an equation. The following are equivalent.

   a. $\mathcal{K} \models p\approx q$.

   b. $(p,q)$ belongs to the congruence $\lambda_{\mathcal{K}}$ on $\mathbf{T}(X_\omega)$.

   c. $\mathbf{F}{\mathcal{K}}(X\omega) \models p\approx q$.

   Proof. We shall show (a) $\implies$ (c) $\implies$ (b) $\implies$ (a). Throughout the proof we write $\mathbf{F}$ for $\mathbf{F}{\mathcal{K}}(X\omega)$,$\mathbf{T}$for$\mathbf{T}(X_\omega)$and$\lambda$for$\lambda_{\mathcal{K}}$.

   Recall that $\mathbf{F} = \mathbf{T}/\lambda \in \mathbf{S}\mathbf{P}(\mathcal{K})$. From (a) and Lemma 4.36 (Bergman, 2012) we get $\mathbf{S}\mathbf{P}(\mathcal{K}) \models p \approx q$. Thus (c) holds.

   From (c), $p^{\mathbf{F}}(\bar{x}_1,\dots, \bar{x}_n) = q^{\mathbf{F}}(\bar{x}_1,\dots, \bar{x}_n)$ where $\bar{x}i = x_i/\lambda$. From the definition of$\mathbf{F}$,$p^{\mathbf{T}}(x_1,\dots, x_n) \equiv\lambda q^{\mathbf{T}}(x_1,\dots, x_n)$from which (b) follows since$p = p^{\mathbf{T}}(x_1,\dots, x_n)$and$q = q^{\mathbf{T}}(x_1,\dots, x_n)$.

   Finally assume (b). We wish to apply Lemma 4.37. Let $(A, f^A) \in \mathcal{K}$ and $h \in \operatorname{Hom}(\mathbf{T},(A, f^A))}}$. Then $\mathbf{T}/\ker h \in \mathbf{S}((A, f^A)) \subseteq \mathbf{S}(\mathcal{K})$ so $\ker h \supseteq \lambda$. Then (b) implies that $h(p) = h(q)$ hence (a) holds, completing the proof.

   Remark. The last result tells us that we can determine whether an identity is true in a variety by consulting a particular algebra, namely $\mathbf{F}(X_\omega)$. Sometimes it is convenient to work with algebras free on other generating sets besides $X_\omega$. The following corollary takes care of that for us.

4. Let $\mathcal{K}$ be a class of algebras, $p$ and $q$ $n$-ary terms, $Y$ a set and $y_1, \dots, y_n$ distinct elements of $Y$. Then $\mathcal{K} \models p \approx q$ if and only if $p^{\mathbf{F}{\mathcal{K}}(Y)}(y_1, \dots, y_n) = q^{\mathbf{F}{\mathcal{K}}(Y)}(y_1, \dots, y_n)$. In particular,$\mathcal{K} \models p \approx q$if and only if$\mathbf{F}_{\mathcal{K}}(X_n)\models p \approx q$.

   Proof. Since $\mathbf{F}{\mathcal{K}}(Y)\in \mathbf{S}\mathbf{P}(\mathcal{K})$, the left-to-right direction uses the same argument as in Theorem 4.38 (Bergman, 2012) (Result 3 in this section). So assume that$p^{\mathbf{F}{\mathcal{K}}(Y)}(y_1, \dots, y_n) = q^{\mathbf{F}_{\mathcal{K}}(Y)}(y_1, \dots, y_n)$. To show that$\mathcal{K} \models p \approx q$, let$(A, f^A) \in \mathcal{K}$and$a_1$,$\dots$,$a_n \in A$. We must show$p^{(A, f^A)}(a_1, \dots, a_n) = q^{(A, f^A)}(a_1, \dots, a_n)$.

   There is a homomorphism $h\colon \mathbf{F}{\mathcal{K}}(Y) \to (A, f^A)$such that$h(y_i) = a_i$for$i \leq n$. Then \begin{align*} p^{(A, f^A)}(a_1, \dots, a_n) &= p^{(A, f^A)}(h (y_1), \dots, h (y_n)) = h(p^{\mathbf{F}{\mathcal{K}}(Y)}(y_1, \dots, y_n))\ &= h(q^{\mathbf{F}_{\mathcal{K}}(Y)}(y_1, \dots, y_n)) = q^{(A, f^A)}(h(y_1), \dots, h(y_n))\ &= q^{(A, f^A)}(a_1, \dots, a_n).\end{align*} It follows from Lemma 4.36 (Result 1 of this section) that every equational class is a variety. The converse is Birkhoff’s Theorem.

Theorem (Bergman, Thm 4.41) Every variety is an equational class.

Proof. Let $\mathcal{W}$ be a variety. We must find a set of equations that axiomatizes $\mathcal{W}$. The obvious choice is to use the set of all equations that hold in $\mathcal{W}$. To this end, take $\Sigma = \operatorname{Id}(\mathcal{W})$. Let $\overline{\mathcal{W}} = \operatorname{Mod}(\Sigma)$. Clearly, $\mathcal{W} \subseteq \overline{\mathcal{W}}$. We shall prove the reverse inclusion.

Let $(A, f^A) \in \overline{\mathcal{W}}$ and $Y$ a set of cardinality $\max(|A|, |\omega|)$. Choose a surjection $h_0\colon Y \to A$. By Theorem [thm:4.21], $h_0$ extends to a (surjective) homomorphism $h \colon \mathbf{T}(Y) \to (A, f^A)$. Furthermore, since $\mathbf{F}{\mathcal{W}}(Y) = \mathbf{T}(Y)/\Theta{\mathcal{W}}$, there is a surjective homomorphism$g \colon \mathbf{T}(Y) \to \mathbf{F}_{\mathcal{W}}$.

We claim that $\ker g \subseteq \ker h$. If the claim is true then by Lemma [ex:1.26.8] there is a map $f\colon \mathbf{F}{\mathcal{W}}(Y) \to (A, f^A)$such that$f {\circ}}g = h$. Since$h$is surjective, so is$f$. Hence$(A, f^A) \in \mathbf{H}(\mathbf{F}{\mathcal{W}}(Y)) \subseteq \mathcal{W}$ completing the proof.

Let $u,v \in T(Y)$ and assume that $g(u) = g(v)$. Since $\mathbf{T}(Y)$ is generated by $Y$, by Theorem [thm:4.21], there is an integer $n$, terms $p, q \in T(X_n)$, and $y_1$, $\dots$, $y_n \in Y$ such that $u = p^{\mathbf{T}(Y)}(y_1,\dots, y_n)$ and $v = q^{\mathbf{T}(Y)}(y_1,\dots, y_n)$, by Theorem [thm:4.32]. Applying the homomorphism $g$, $$p^{\mathbf{F}{\mathcal{W}}(Y)}(y_1,\dots, y_n) = g(u) = g(v) = q^{\mathbf{F}{\mathcal{W}}(Y)}(y_1,\dots, y_n). $$Then by Result 4 above (Corollary 4.39, Bergman, 2012), $\mathcal{W} \models p \approx q$, hence $(p \approx q) \in \Sigma$. Since $(A, f^A) \in \overline{\mathcal{W}} = \operatorname{Mod}(\Sigma)$, we get $(A, f^A) \models p \approx q$. Therefore,$$ h(u) = p^{(A, f^A)}(h_0(y_1), \dots, h_0(y_n)) = q^{(A, f^A)}(h_0(y_1), \dots, h_0(y_n)) = h(v),$$ as desired.