The Palfy-Saxl Problem

February 13, 2015 Reading time: about 1 minute (333 words).

Suppose the lattice shown below is a congruence lattice of an algebra.

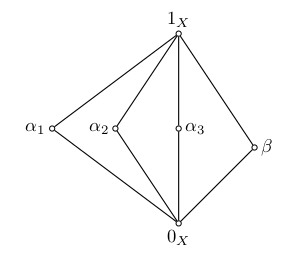
Conjecture: If the three $\alpha_i$ 's pairwise permute, then all pairs in the lattice permute.

Whether or not this claim is true is a simplified version of a question left open by Pálfy and Saxl at the end of their 1990 paper. Below is a more formal statement of the problem, and a link to my notes describing a proposed method of solution. There remains one gap in the proof, that I'm not yet sure how to fill, but I am hopeful that the overall strategy will work.

🔗 Graphical composition

In an attempt to prove the claim above and its generalization, I apply an idea described in Heinrich Werner's paper called graphical composition.

🔗 The Problem

Before giving a more precise statement of the problem, let us recall a couple of basic definitions. Given two equivalence relations $\alpha$ and $\beta$ on a set $X$ , the relation

$\alpha \circ \beta = {(x,y) \in X^2: (\exists z)(x ; \alpha ; z ; \beta ; y)}$

is called the composition of $\alpha$ and $\beta$ , and if $\alpha \circ \beta = \beta \circ \alpha$ then $\alpha$ and $\beta$ are said to permute.

Problem. $\def\bA{\bf A} \def\bB{\bf B}$ Let $\bA$ be a finite algebra with $\operatorname{Con} \bA$ isomorphic to $M_n$ , for some $n\geq 4$ . If three nontrivial congruences of $\bA$ pairwise permute, does it follow that every pair of congruences of $\bA$ permute?